
 |
|
Optimised design of injection moulds by three-dimensional calculation with volume elements |
|
From
filling to warpage in 3D
|
|
Andi
Clements
|
|
Rapra
Technology Ltd
|
| For many
injection-moulded parts, 3D simulation has definite advantages over calculations
using 2 ½ dimensional shell models. This article provides an overview
of the new possibilities offered by the Sigmasoft simulation program.
In the development
of injection-moulded parts, increasing use is being made of simulation
programs which are able to calculate the mould filling, the holding pressure
phase and cooling phase right up to demoulding, including the warpage
of the part [1, 2]. The programs used to date for the simulation of injection
moulding processes work with geometrical information which approximately
describe the upper, lower or central surfaces of the actual geometry.
This calculation procedure is generally referred to as a 2 ½ dimensional
shell model. The only approximate description of the part geometry by
a central surface could have a detrimental influence on the quality of
the result. This is particularly the case with calculations for components
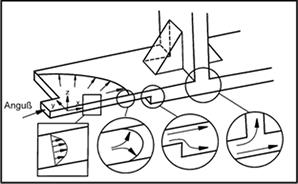
with non-uniform wall thicknesses [3, 4, 5, 6]. Figure 1 shows schematic
areas in a plastic part in which three-dimensional flow effects take place
[4]. |
|
Figure
1
|
 |
|
Completely three-dimensional approaches to simulation for calculating flow processes have been described before. However, it has recently become possible to calculate not only the fibre orientation but also the warpage of fibre-reinforced components using three-dimensional methods. The mould
in a 3D volume model |
|
Figure
2
|
 |
|
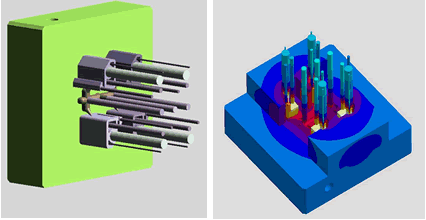
In Sigmasoft the mould is three-dimensionally meshed. Figure 2 shows the structure of a mould in individual parts, including the cooling. Several cycles may be simulated in order to determine the temperature conditions of the mould in quasi-stationary state. This method enables corner effects to be calculated physically and the local impact on the part, for example on warpage, to be allowed for in the correct manner. |
|
Figure
3
|
 |
|
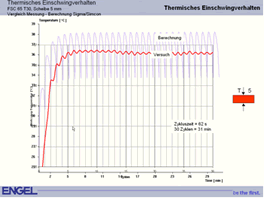
In Figure 3 shows the calculated temperature profile for an actual mould in a direct comparison with measurements in the factory of the injection moulding manufacturer Engel. In addition to the exact temperatures, it was also possible to predict exactly the number of cycles during the start-up process. Overmoulding
injection moulding and insert injection moulding |
|
Figure
4
|
Figure
5
|
Figure
6
|
 |
 |
 |
|
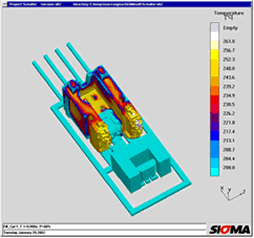
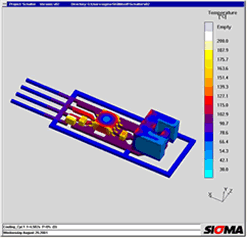
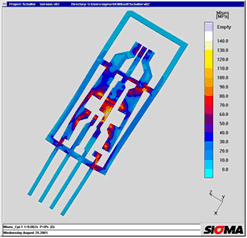
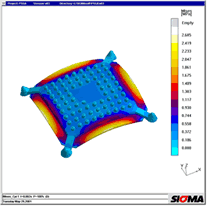
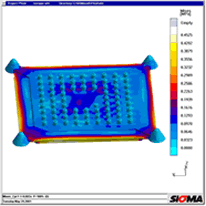
Figures 4 to 6 show the simulation of a switch component in which electronic components are encapsulated by a thermoplastic material. The geometry was transferred from a CAD system. Figure 4 shows the mould filling, Figure 5 shows the parts to be encapsulated. The arrow indicates a component which became detached during the injection process. The plastic melt flow heats up the solder and weakens the connection with the diode and the printed circuit board. The increased temperature results in stresses additional to the injection pressure and thermal warpage in the components and the printed circuit board (Figure 6), which also contribute to failure. Build-up
of internal stresses with a PSGA (polymer stud grid array) |
|
Figure
7
|
Figure
7 (Expanded)
|
 |
 |
|
Figure
8
|
Figure
9
|
Figure
10
|
 |
 |
 |
|
Warpage
in thick-walled components |
|
Figure
11 (And inset -actual
part)
|
Figure 12 |
 |
 |
|
|
|
Predicting
warpage in fibre-reinforced materials |
|
Figure
13a
|
Figure 13b | Figure 13c |
 |
 |
 |
|
Figure 13a shows the mould filling for a fibre-reinforced component for medical equipment. Gating from above produces different fibre orientations in the thick-wall area (Figure 13b). The colours represent the degree of orientation. Light colours indicate a high degree of orientation while dark areas represent areas with a distributed fibre orientation. While the lower area has a strong alignment in the direction of the x-axis, the upper area is orientated in the direction of the y-axis. During cooling, therefore, warpage in a longitudinal direction during cooling will essentially take place transversely to the fibre orientation in the upper area and longitudinally to the fibre orientation in the lower area. This causes the part to warp (Figure 13c). |
|
If, on the other hand, the gate position is optimised and the mould filling performed from the end (Figure 14a), a symmetrically fibre orientation will become established in the thick-walled area (Figure 14b). This means that warpage occurs uniformly in the longitudinal direction and the part remains straight (Figure 14c). |
|
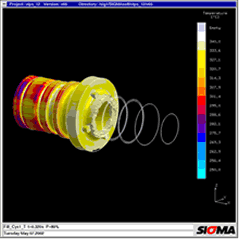
Figure
14a
|
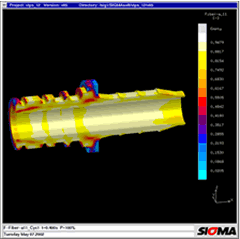
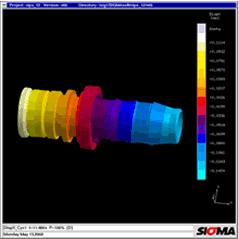
Figure 14b | Figure 14c |
 |
 |
 |
|
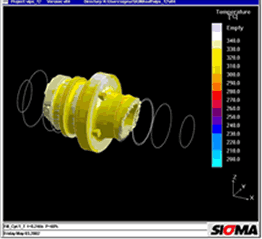
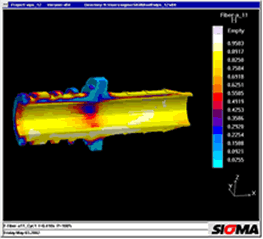
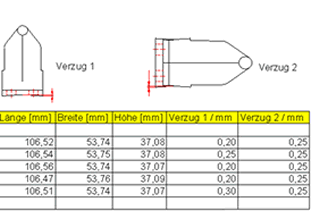
Figure 15 shows another example of a warpage calculation. This is a relatively large pump housing made of fibre-reinforced polyamide. Once again, simulation confirmed the warpage of the part. Conformity between the calculated warpage values and real values was demonstrated by work performed in cooperation with the company Lüttgens in Germany. The warpage values were measured on a real component and compared with calculated values (Figure 16). In all cases, the differences were only slight and confirmed the great potential of warpage calculations in 3D volume models. |
|
Figure
15
|
|
 |
 |
 |
 |
| Figure 16- Simulation and measurements (below) of anisotropic shrinkage and warpage | |
 |
|
Interfaces
with FE programs Outlook
The quantitative calculation of warpage in fibre-reinforced parts in 3D is the subject of ongoing development work [10]. The objective is to make a tool available in the near future which may be used to predict warpage so accurately that part geometry may be optimised at the early design stage and the appropriate mould provided.
|
|
References [1] Bogensperger,
H.: Overview - experience with injection moulding simulation. Kunststoffe
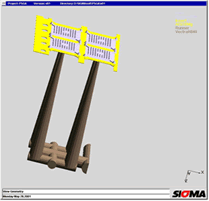
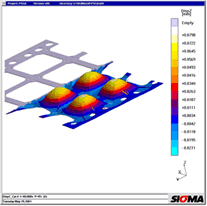
85 (1995) 1, p 44 et seq. Figure 1: Areas of three-dimensional melt flow during injection moulding. The main drawback of 2 ½ D approaches is that flow movements in the direction of part thickness and friction in the flow plane are ignored [4] Figure 2: The calculation of the exact temperature distribution in all areas of the mould is the basis for the correct prediction of filling, shrinkage and warpage Figure 3: Comparison of calculated and measured temperatures over 30 cycles during the start-up process. The measured curves were transferred manually and have a low amplitude due to the inertia of the thermocouples. The start-up behaviour of six cycles to steady-state was confirmed. Photograph: Engel Figure 4: Temperature distribution during filling. The pressure distribution and the heating-up of the electronic components were calculated in 3D Figure 5: Local temperature distribution in the encapsulated components reveals local overheating; the soldered joint reaches temperatures of up to 160 °C Figure 6: The temperature increase results in thermal warpage in the printed conductor. The deformation, exaggerated here, may result in the failure of the connection between the printed circuit board and electronic components Figure 7: PSGA injection moulded part and lead frame Figure 8: Thermally induced warpage - shown greatly exaggerated - for injection moulded part and lead frame Figure 9: Warpage and von Mises internal stresses due to non-uniform cooling at the edge Figure 10: Reduced von Mises internal stresses with optimised geometry Figure 11: Thick-walled polyethylene flange and greatly exaggerated representation of warpage. Photo: Friatec Figure 12: The warpage in Figure 11 may be attributed to the non-uniform temperature distribution "corner effect" (yellow and red areas) during cooling to room temperature Figure 13a: Mould filling with gate position at top Figure 13b: Fibre orientation in y-direction: the gate position at the top results in different fibre orientations in the thick-walled areas at the top and bottom Figure 13c: During cooling, thermal expansion in the longitudinal direction is determined from the different expansion coefficients in the upper and lower areas, one transverse to and one longitudinal to the fibre orientation, cf Figure 13 b, resulting in warpage Figure 14a: With a modified gate position, filling takes place uniformly in the thick-walled area Figure 14b: Fibre orientation in x-direction for modified version: the rear gate position achieves uniform fibre distribution in the longitudinal direction Figure 14c: With a modified gate position, the thermal expansion is the same at the top and bottom and the part remains straight Figure 15: Warpage calculated in the 3D volume model for a fibre-reinforced pump housing in a direct comparison with the part. Warpage in the right-hand diagram is greatly exaggerated Figure 16: The comparison between measured and calculated warpage values reveals close correlation. The calculated values for warpage 1 are 0.2 mm and those for warpage 2 are 0.25 mm |
| View
the original document
in PDF format here: (Log in to the members-only area and obtain your personal copy from the download centre) |
File Size: 1Mb |